10 Important Short Tricks of Profit And Loss Problems

 Basic Concept of Profit and Loss Problems:

• Cost Price (CP) –> Price at which an article is Purchase
• Marked Price (MP) –> Price written on the article/MRP
• Selling Price (SP) –> Price at which an article is sold
• Profit –> SP> CP                Profit = SP – CP
• Loss –> CP> SP                 Loss = CP – SP
• Profit% or Gain % –> Profit /CP ×100% = SP – CP / CP ×100%
• Loss% –> Loss/CP ×100% = CP – SP / CP×100%

Rule of Fraction in Profit and Loss Problems:

The gain of x% –> Calculate figure –> 100& 100 + x

The loss of x% –> Calculate figure –> 100& 100 – x

Profit and Loss Problems Example:

(A) If CP = 50, Gain % = 5 then SP = ?

Calculate figure –> 100& 105

SP = 50 ×105/100 = 52.5

(B) If CP = 50, loss % = 5 then SP = ?

Calculate figure –> 100& 95

SP = 50 × 95/100 = 47.5

Type 1:

If two articles are sold- the first article at x% profit and the second article at y% loss, thus making no profit, no loss in the transaction,

Then cost price of the two articles are in the ratio y: x

Proof: Let cost price of two articles is Rs.a and Rs.b respectively.

Then profit on the first article = ax/100 and loss on the second article = by/100

There is no profit or no loss in the bargain. –> ax/100 = by/100 –> ax=by –> a/b = y/x

Profit and Loss Problems Example:

1) A man purchased two articles for a total cost of Rs.9000. He sold the first article at 15% profit and the second at 12% loss. In the bargain, he neither gained nor lost anything. Find the cost price of the first article.

a) Rs. 4000   b) Rs.4500   c) Rs.5000    d) Rs.5500

Solution:

The ratio of the cost price of the first and the second article = 12: 15 = 4: 5

Cost price of the first article = 4/9 ×9000 = Rs.4000

Type 2:

On selling an article for Rs.x, a person earns a% profit. In order to earn b% profit, he must sell the article for Rs.x ×(100+b) / (100+a),

i.e. New selling price = (Old selling price × (100 + Desired profit (in%))/ (100+ Initial profit (in%))

Profit and Loss Problems Example:

1) On selling an article for Rs.550, a man gains 10%. What should be the selling price, if desired profit is 20%?

a) Rs.500    b) Rs.600    c) Rs.660    d) Rs.715

Solution:

SP= 550×(100 + 20 / 100 +15)

= 550 × 120/110 = Rs.600

2) Ram sold a cow for Rs.136 and thus lost 15%. At what price he should have sold it to gain 15%?

a) Rs.180   b) Rs.150   c) Rs.200   d) Rs.184

Solution:

New selling price = 136 × (100+15)/(100-15)

= 136 × 115/85 = Rs.184

 

Type 3:

1) Shopkeeper buys 25 tables and 10 chairs for Rs. 7000 sells, table at 10%, chair at 12% profit. If he gets 7740 find CP of table and chair?

Solution:

(If Both Increase by 10% then overall increment will be 10% i.e. 10% of 7000/- which is Rs.700. But profit = 740. This extra 40/- is due to 2% of chair)

2% Chair –> 40/-

100% C(10) –> 2000

1 chair = 2000/10 = 200

So all table (25) = 5000/-

1 table = 5000/25 = 200/-

Type 4:

If the price of an article is marked x% above the cost price and x% discount is allowed on its marked price, the loss percent = x²/100

Profit and Loss Problems Example:

1) A shopkeeper mark price of his article 12% above the cost Price and then allows a 12% discount on the marked price. What is his loss percent?

a) 0%    b) 1%   c) 1.44%   d) 2.4%

Solution:

Loss% = 12²/100 = 1.44%

Type 5:

If two articles are sold for the same selling price. On selling the first article, a man gains x% and on selling the other article he lose x%, in such cases there will be always loss, and Loss% = x²/100 or (Common gain and loss)²/100

Profit and Loss Problems Example:

1) A TV manufacturer sells two televisions at Rs.9900 each. He earned a profit of 10% on the first one and suffered a 10% loss on another. His net profit or loss percent is?

a) 1% loss    b) 1% gain   c) 2% loss   d) No profit/loss

Solution:

Loss% = (Common gain and loss)²/100

= 10²/100 = 1%

Type 6:

If two articles are sold for the same selling price. On selling the first, the gain is x% and on selling the second the gain is y%, then net % profit

= (2× (100+x) (100+y)/ (100+x) + (100+y)) – 100

Profit and Loss Problems Example:

1) A man sold two articles for Rs.600 each. On selling first, he gains 20%, and on the other, he gains 30%. What is the profit percent in the transaction?

a) 24.8%    b) 25%   c) 50%     d) 56% 

Solution:

Profit% = (2×120×130 / 120+130)-100 = 24.8%

Type 7:

1) A shopkeeper buys 2 chairs at a total cost of 900/-. By selling one at 4/5 of its cost and the other at 5/4 of its cost he made a profit of 90/-. Find CP of each chair

Solution:

4/5 = 80% i.e.20%loss

5/4 = 125% i.e = 25% profit

Profit = 90/- i.e 10% (90 is 10% of 900)

i.e Ratio of their CP = 15 : 30 = 1:2

1^stchair = Rs. 300, 2^nd chair = Rs. 600/-

Type 8:

1) A man purchases 11 orange for Rs.10/- and sell them at the rate of 10 oranges for Rs.11/. Find profit?

Solution:

Profit = (11×11 – 10×10 / 10×10)×100%

= 21%

Type 9:

1) Selling price of two articles 4000/- each. First article sold at a profit of 25% profit and 2^nd article at some % loss. Find loss % on 2^ndarticle if there is neither loss nor gain.

Solution:

Type 10:

1) How much % more than CP must a shopkeeper mark his goods to gain 26% after giving a discount of 10%

Solution:

=100×126/100×100/90

=140

Difference =140 -100 =40%

More Useful Shortcuts on Profit and Loss:

1). The cost price of 20 articles is equal to the selling price of 18 articles, then profit %

PROFIT = DIFFERENCE /SP *100 =2/18*100 =100/9 =11   1/9%

2). Nick sold a machine to Sonia at a profit of 30% and Sonia sold it to Varun at 20%loss. If nick get the machine for 5000 then what is the cost price of the machine at Varun?

PERCENTAGE EFFICIENCY = (+30-20 *(+30*-20 /100) =4%

5000 -100  ; 104- 5200

Cp of varun =5200

3). If a shopkeeper sells goods 6%loss on cost price but gives 14 g instead of 16g. What is his percentage of profit or loss?

A=6%  , c=16g b=14g

FORMULA = [(100-A) (C/B)-100] %

= 94 *(16/14) -100 % =52/7% gain

4). A dealer sold at 20% loss on cost price but uses 40% less weight. What is his percentage of profit or loss?

FORMULA =B±A / (100-B) 
=    40 -20 / (100 -40)
=    20/60=2/6*100%
=     33 1/3 %  profit

5). If 2/3 of the article  sold at 30% profit 1/4 of part at 16%, profit and remaining part of 12% Profit  finally, there is a profit of rs.75, then the cost price of the article

A=2/3 ,x=30%, b=1/4, y =16% , z =12%,R=75

C= 1-(1/2+3/4) =1/12

COST PRICE OF ARTICLE =R*100 / (AX +BY+CZ)

= (75*100) / ((2/3*30)(1/4*16) (1/12*12)

=7500/25 =300

6). A bought a certain quantity of oranges at a total cost of 1200. He sold 1/3 of those oranges at a 20% loss. If A earns an overall profit of 10%, At what percentage of profit did A sell the rest of the oranges?

Sol:-

1/3 of oranges sold, Remaining we have 2/3 of oranges. So,
1/3:2/3=>1:2. Final ratio is 1:2
He sold 1/3 of those oranges at 20% loss and overall profit of 10%, so we using mixture allegation method,

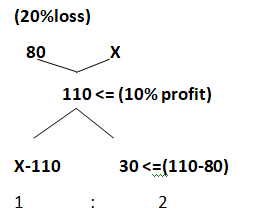
X-110/30=1/2

We solve these, we get X=125

So A sell the rest of the oranges at 25% profit.

7). If a shopkeeper sells an item for 1410, his loss is 6%. To earn a profit of 15% he should sell it for?

Sol:

(100-loss)/sp1=(100+gain)/sp2
=>94/1410=115/x
=>94x=115*1410
=>x=1725

8). By selling 25% of a quantity of sugar a person earns 40% profit, While on the remaining quantity he incurs a loss of 20%. Find the overall profit/loss percentage.

Sol:

Profit/loss%= (25/100)*40% +(75/100)*(-20%)

=>(1/4) *40% +(3/4)*(-20%)

=>10%+(-15%)

=> (-5%)

So, 5% loss. (‘-‘ symbol denotes a loss)

If You Have Any Queries, Feel Free to Ask us in the below Comment Section.