Concept of Quadrilateral and their relationship for SSC and Railway : Mathematics

Quadrilateral

A plane figure bounded by four line segment is called the quadrilateral. The area enclosed by the four sides must not be zero.

A simple quadrilateral has four sides and four angles.

Sum of the angle of the quadrilateral is always 360°

∠A+∠B+∠C+∠D=360°

Area of quadrilateral ABCD = 1/2[AC(DE+BF)]

DE and BF are the perpendiculars on diagonal AC.

Diagonals bisect each other.

Diagonals need not be perpendicular or equal.

Each diagonals divides a parallelogram into two triangle ofequal area.

Area of a parallelogram is double the area of the triangle formed by diagonals.

Bisectors of the angle of a parallelogram form a rectangle.

A parallelogram inscribed inside a circle is rectangle.

A parallelogram circumscribed about a circle is a rhombus.

AC²+BD²=AB²+BC²+CD²+AD²=2(AB²+BC²)

Area of parallelogram ABCD= Base *Height

A parallelogram is a rectangle if its diagonal are equal.

Parallelogram that lies on the same base and between the same parallel lines are equal in area.

area of  Parallelogram ABCD=Area of Parallelogram ABPQ

If a triangle and a parallelogram are on the same base and between the same parallel lines, the area of triangle is half of the parallelogram.

Area of triangle APB=1/2(area of parallelogram ABCD)

Rectangles:

A rectangle is a parallelogram whose all angles 90°.

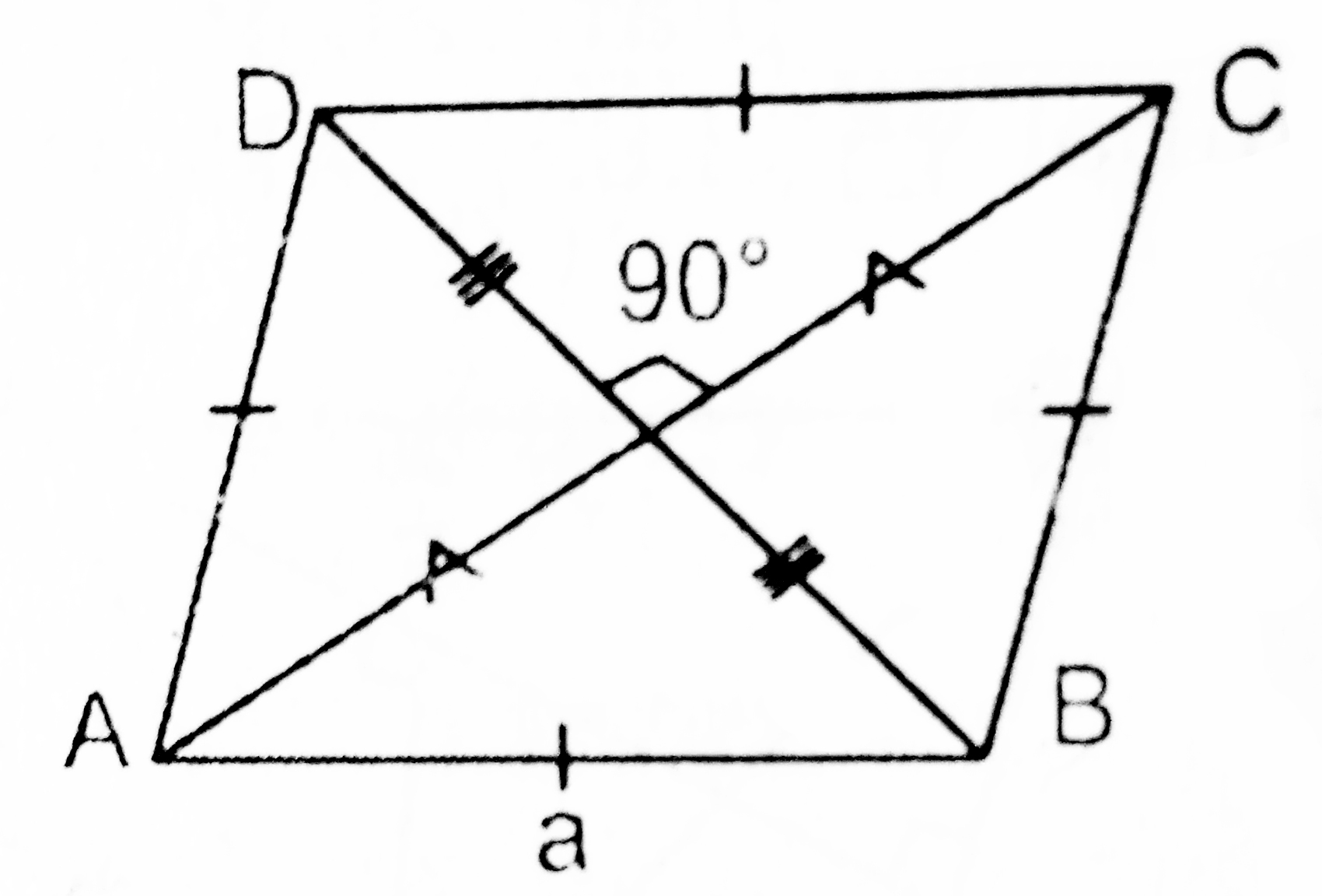
Diagonals are equal and bisect each other but not necessarily at 90°.

A square has maximum area for a given perimeter of rectangles.

Figures formed by joining the midpoints of the adjacent side of the rectangle is a rhombus.

Angle Bisectors of a rectangle form another rectangle.

Area of rectangle=length*breadth

Diagonals of the rectnagle[AC=BD=√(l²+b²)]

Square:

A square is a rectangle with all its side equal and all the angle equal to 90°.

Diagonals are equal and bisect each other at 90°

Figure formed by joining the midpoint of the sides of square is a square.

Area= a²

Diagonal=√2*a

Rhombus:

A parallelogram having all its sides equal is a rhombus.

Diagonals of the rhombus bisect each other at a right angle but they are not necessarily equal.

A rhombus may or may not be a square but all the square are rhombus.

The figure formed by joining the midpoint of the adjacent sides of a rhombus is a rectangle.

A parallelogram is a rhombus if its diagonals are perpendicular to each other.

Area of rhombus=1/2(product of diagonal)

here AC and BD are diagonal.

AC²+BD²=4AB²

Trapezium:

A quadrilateral is a trapezium with only two sides parallel to each other.

The sum of co-interior angles are equal to 180(∠A+∠D=180°, B +C=180)

Area of trapezium =1/2[(sum of parallel sides)*heights]

     = 1/2[(AB+CD)*DM]

sum of the square of diagonal =(sum of square of non-parallel sides) +2(products of parallel  sides)

AC²+BD²=BC²+AD²+2AB*CD

If E and F are the midpoints of two non-parallel sides AD and BC respectively then

EF=1/2(AB+DC)          

AO*OD=OC*BO

E and F are the mid-points of the side AB and AC respectively then,

EF=1/2(BC) and EF parllel BC

Polygon:

A closed figure bounded by three or more than three straight lines.

Convex Polygon:

A polygon in which none of  its interior angle is more than 180°.

Concave Polygon:

A polygon in which at least one of its interior angle is more than 180°

Regular Polygon:

A polygon in which all the sides are equal and also the interior angles are equal is called a regular polygon.

if n is the total no sides of the polygon then

Sum of its interior angle is (n-2)*180°

Each exterior angle=360°/n

Sum of all exterior angle is 360°

Sum of an interior angle and exterior angle is 180°

Number of diagonals =n(n-3)/2